1 次 関数 グラフ 484382-1次関数 グラフ プリント
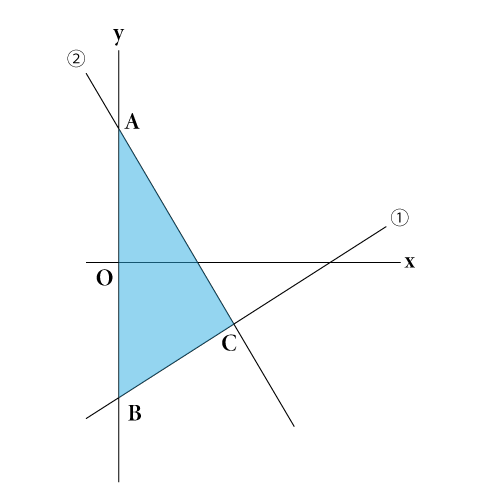
中学2年生数学 1次関数 グラフと図形 長野地区 Itto個別指導学院 長野市の学習塾
Excel。y=2x。一次元方程式のグラフの作り方。 グラフ Excelの研修講座で、先日ご質問があったものの中に、 「一次元方程式のグラフがうまく作れない」 ので、困っているといわれまして。 確かに、通常のようなグラフの作り方では、うまく作ることが出来ないんで一次関数とは、「一次の関数」、つまり「含まれる文字の次数が1の関数」を指します。 比例も一次関数の一種ですが、比例の式に "定数項" が加わったものが一次関数です。 一次関数を表す式: 『y=ax b y = a x b 』 a a 傾き(グラフにした時の直線
1次関数 グラフ プリント
1次関数 グラフ プリント-変化の割合 = 傾き 1次関数 y= axb y = a x b において、 a a は、直線の傾きを表している ことを上で見ました。 この a a には別名があり、 変化の割合 といいます。 変化の割合とは、グラフがどのように変化しているのかを示す値で、 変化の割合 = yの 一次関数とは が の一次式で表されるとき、 は の 一次関数 といいます。 一次関数は、一般的に次のような形で表されます。 一次関数の式にでてくる のことを 傾き(かたむき) のことを 切片(せっぺん) といいます。 あとで一次関数のグラフや式を

一次関数 グラフの書き方 切片が分数のときにはどうする Youtube
1次関数のグラフ 1次関数のグラフは1次関数の式 $ y=ax+b $ の $ x $ と $ y $ の値の変化を直線で表したものです。 線になっていますが、その線上であれば、どの位置でも $ x $ と $ y $ の値を知ることができます。により、1次関数のグラフをかきました。そのときにもグラフが直線になることを見つけま y x x1 x2 y x x1 x2 y x y x 1次関数y=axb の変化の割合が一定であることから、1次関数はいつも 同じペースで変化することがわかります。また、そのために1次関数のグラような方針でグラフをかくのか? 関数ごとにグラフの概形,例えば1次関数は直線,2次関数は放物線,反比例は双曲線な どとわかっているので,ポイントを押さえて必要最小限の点を計算して点をとり,あとはな めらかに結んでいくという方法をとる.
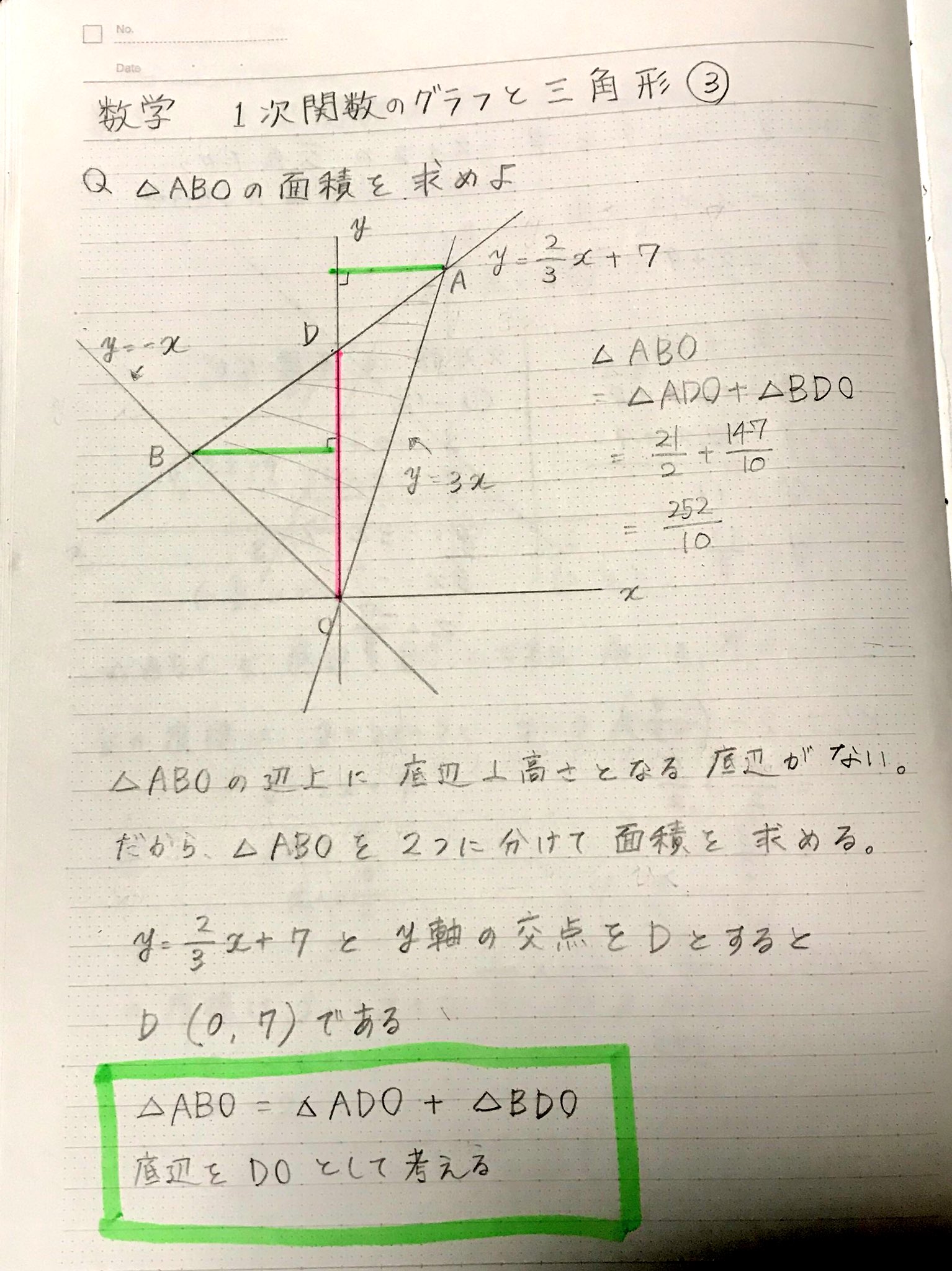
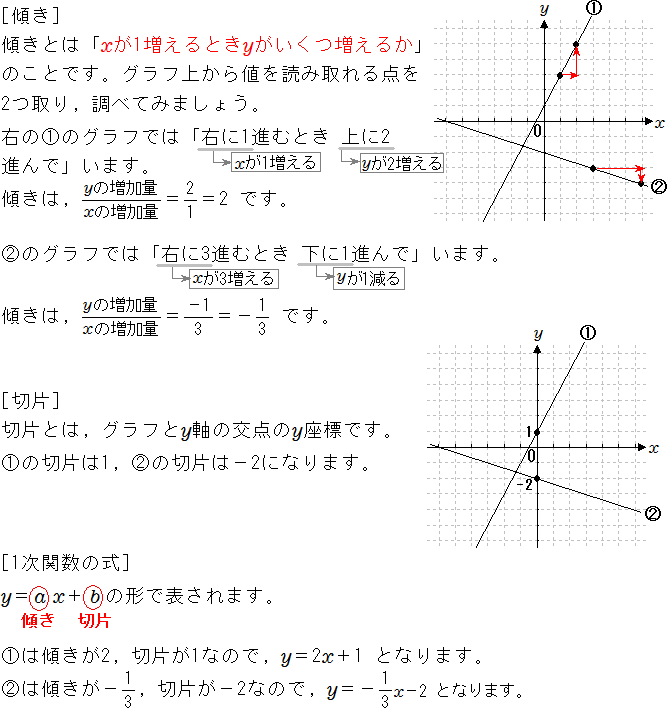
1次関数のグラフ 次の1次関数のグラフはすべて、 y = 2 x のグラフを平行移動してできる。 それぞれ、 x 軸方向、 y 軸方向にいくつ平行移動が行われたのか、式の形から読み取れ。 また、それぞれのグラフを座標平面上に描け。 y = 2 ( x 2) y = 2 ( x 3) − 11次関数 y= a xb のグラフの傾きは a ,切片は b です. (1) 切片 は, y 軸との交点(の y 座標)という「目に見えるもの」なので,切片の意味を間違う生徒は少ないです. 右の図は y=2x1 の直線のグラフで,その切片は赤丸で示した y 軸との交点の y 座標, 1一次関数の式に当てはめていけば完成です。 傾き:\(\frac{2}{3}\) 切片:-1 を式に当てはめて グラフの式は\(y=\frac{2}{3}x-1\)と求めることができました。 このようにグラフから切片と傾きを読み取ることができれば 式を作ることは、とっても簡単です!
1次関数 グラフ プリントのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
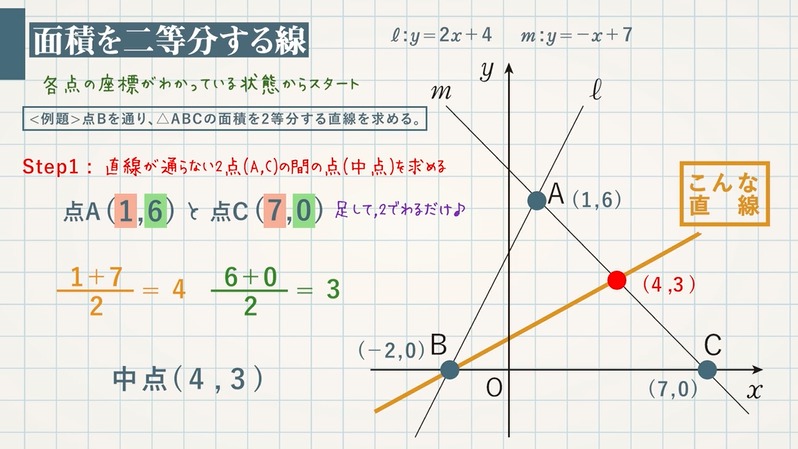
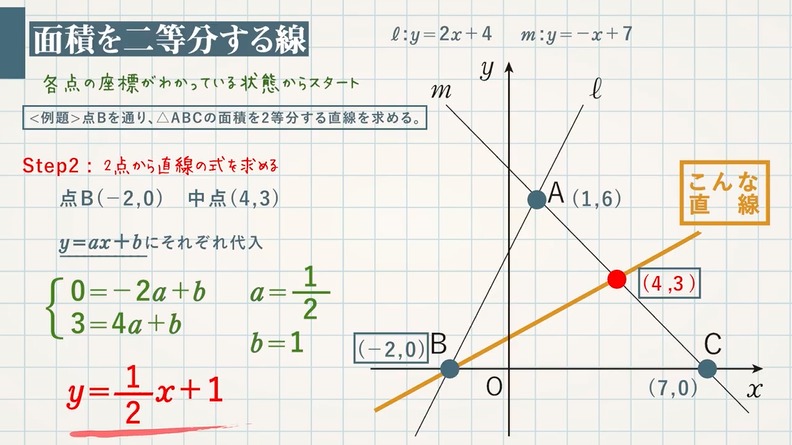
1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |
1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 | 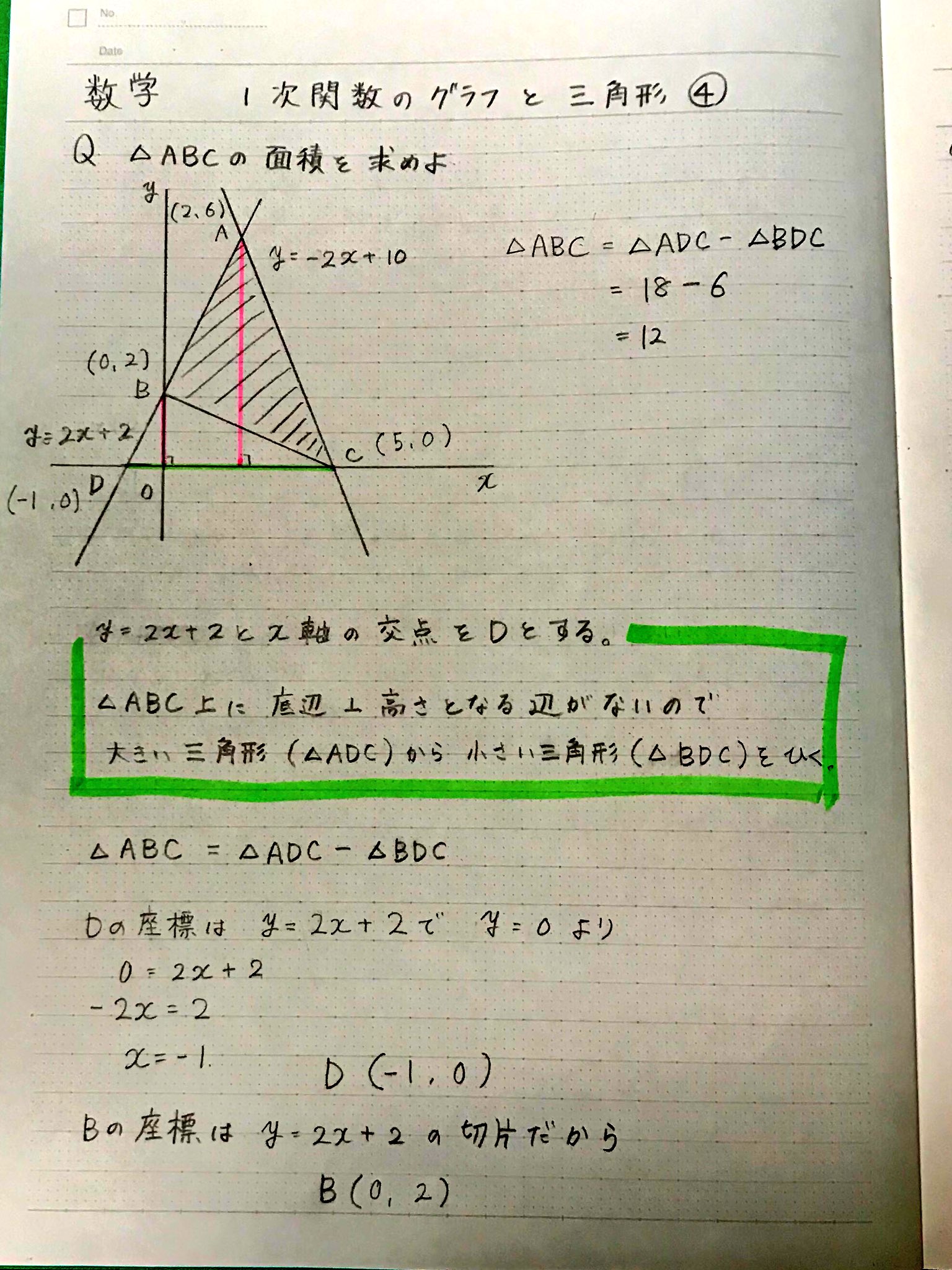 1次関数の交点の座標とグラフから直線の方程式を求める方法 | 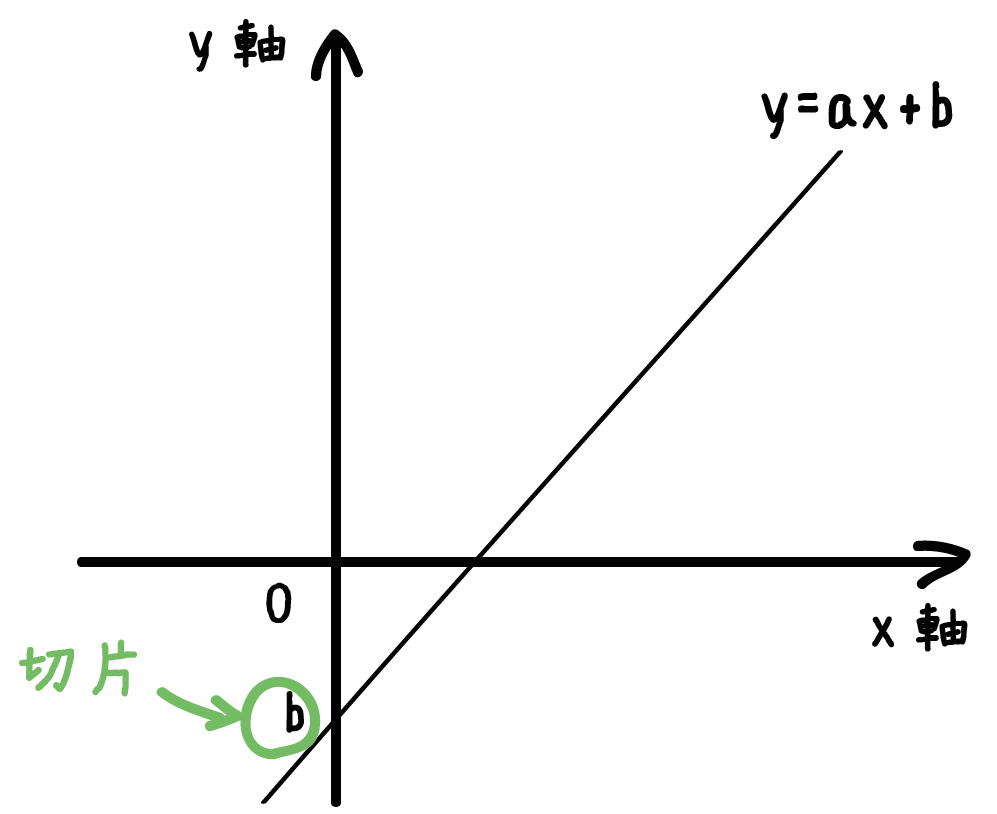 1次関数の交点の座標とグラフから直線の方程式を求める方法 |
1次関数の交点の座標とグラフから直線の方程式を求める方法 | 1次関数の交点の座標とグラフから直線の方程式を求める方法 | 1次関数の交点の座標とグラフから直線の方程式を求める方法 |
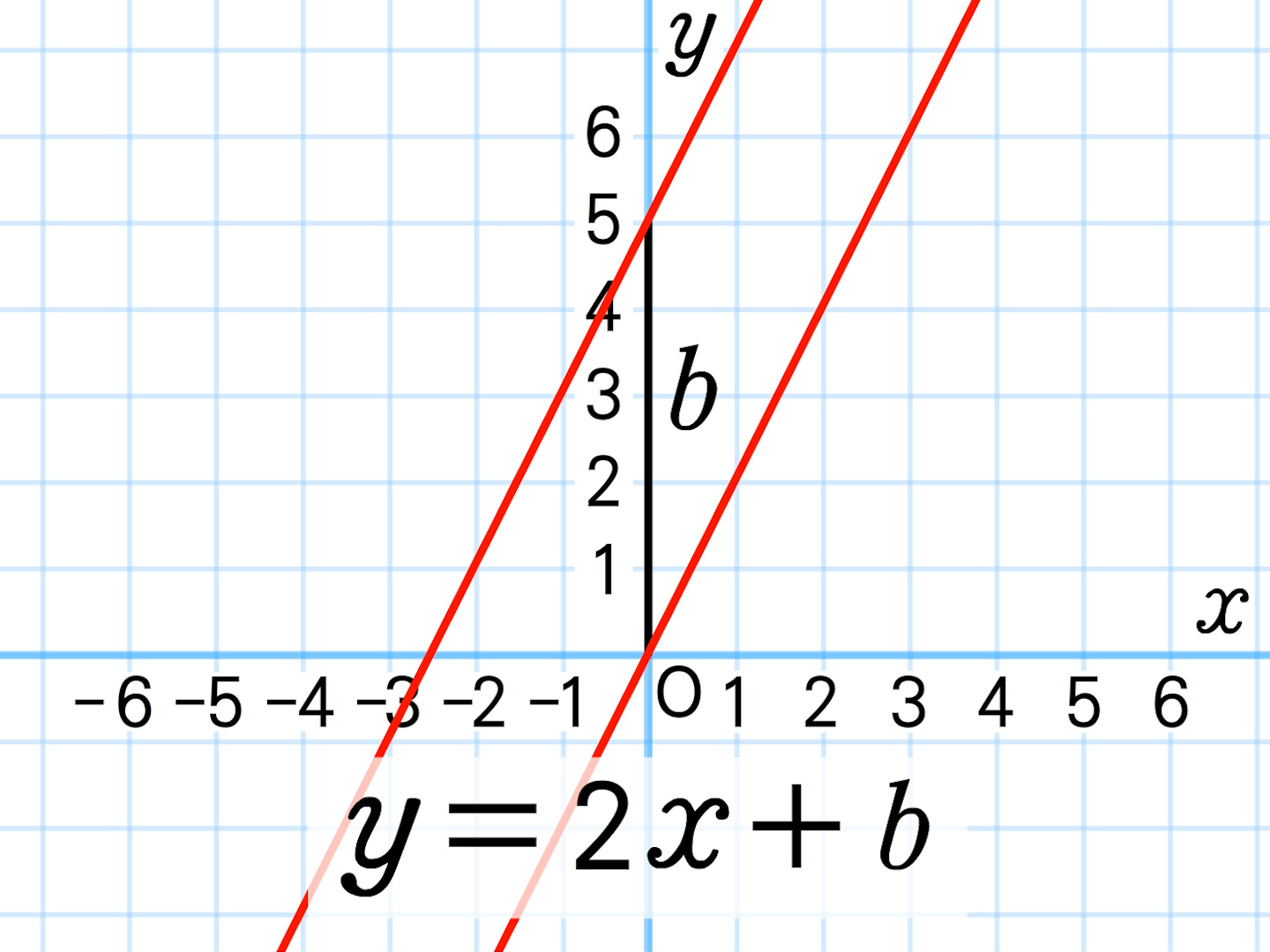 1次関数の交点の座標とグラフから直線の方程式を求める方法 | 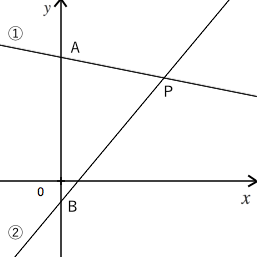 1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 | 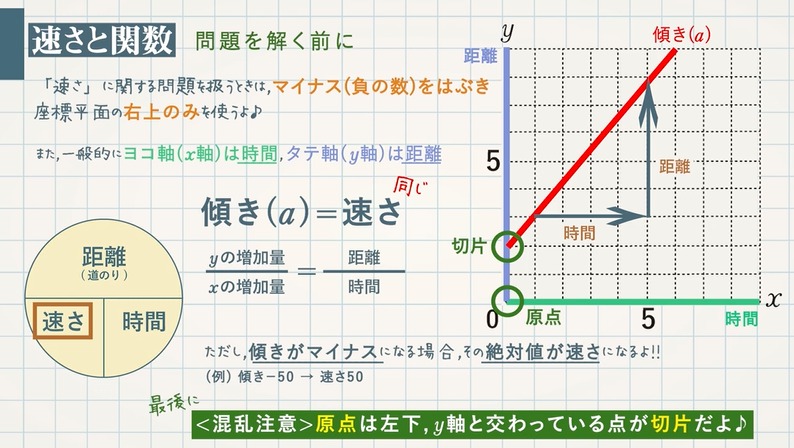 1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 | 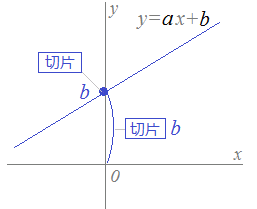 1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 | 1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 | 1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 | 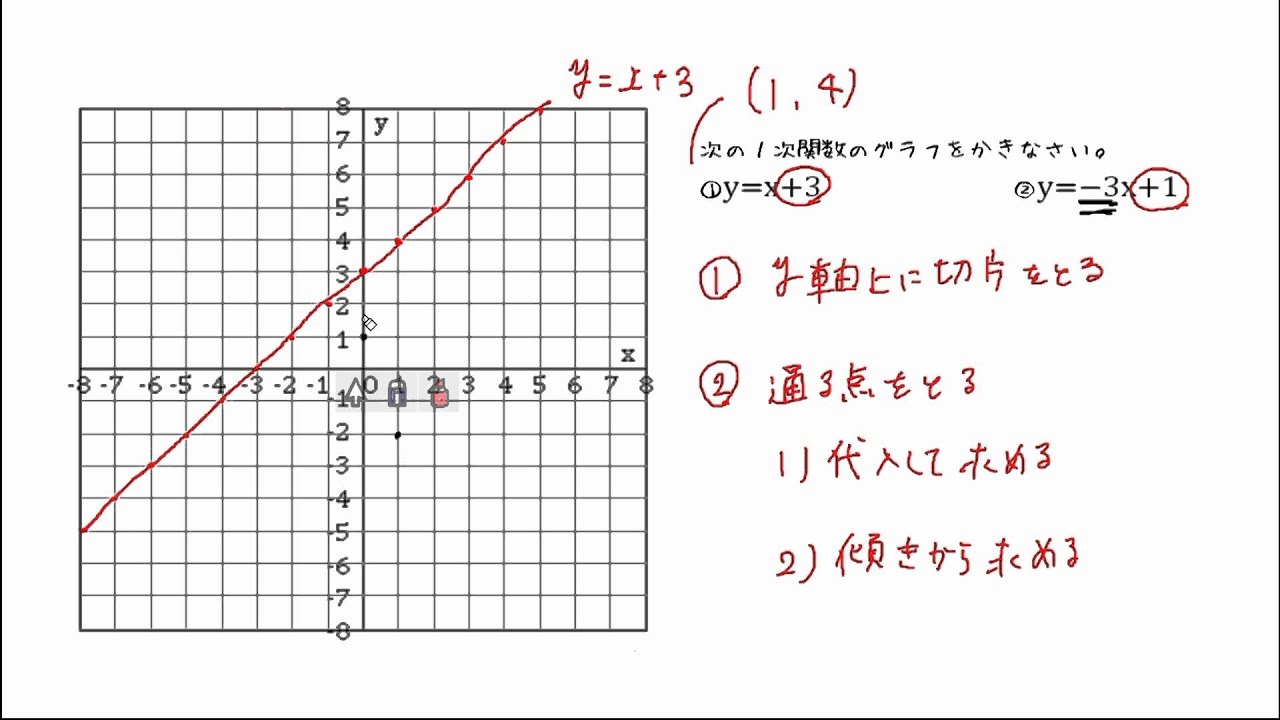 1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 | 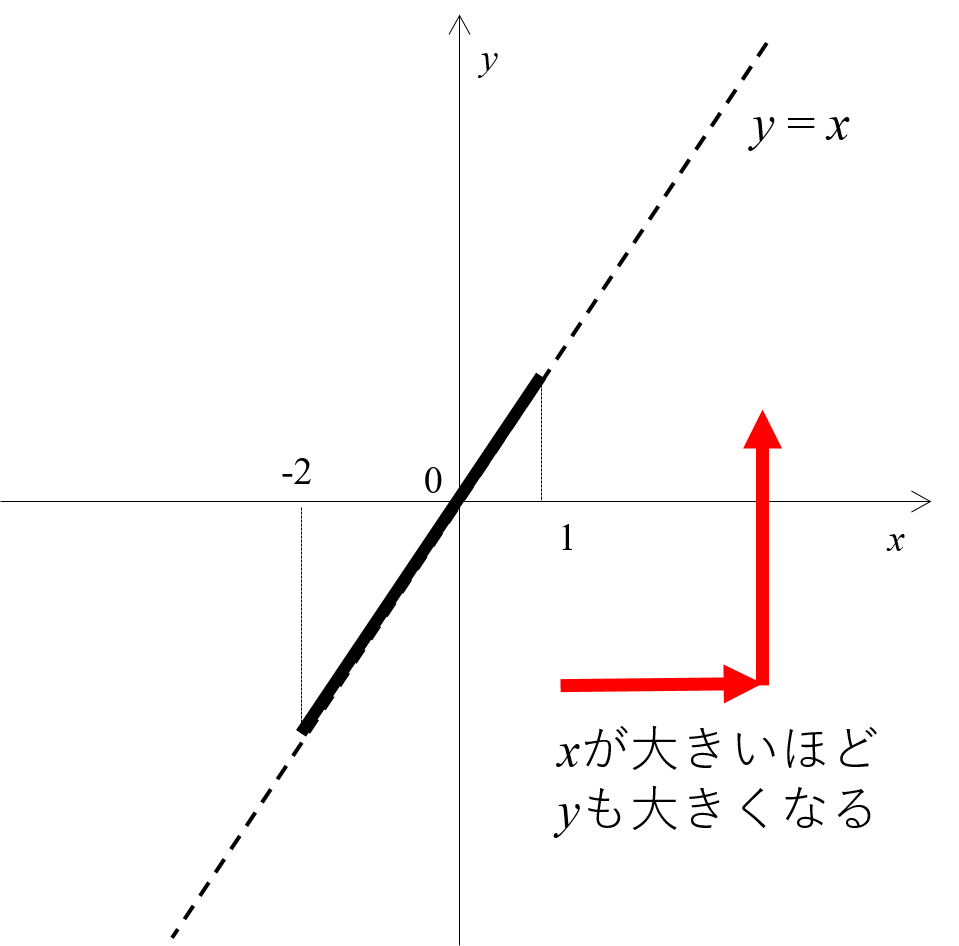 1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 | 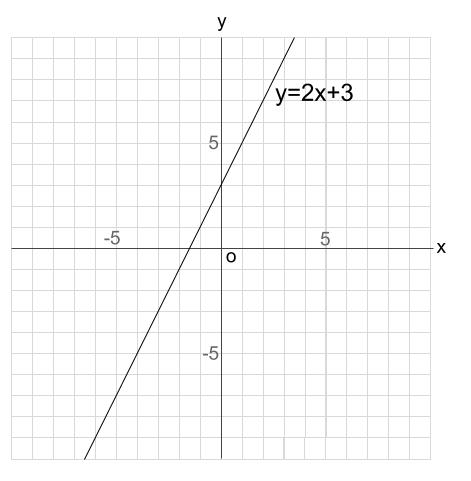 1次関数の交点の座標とグラフから直線の方程式を求める方法 | 1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 | 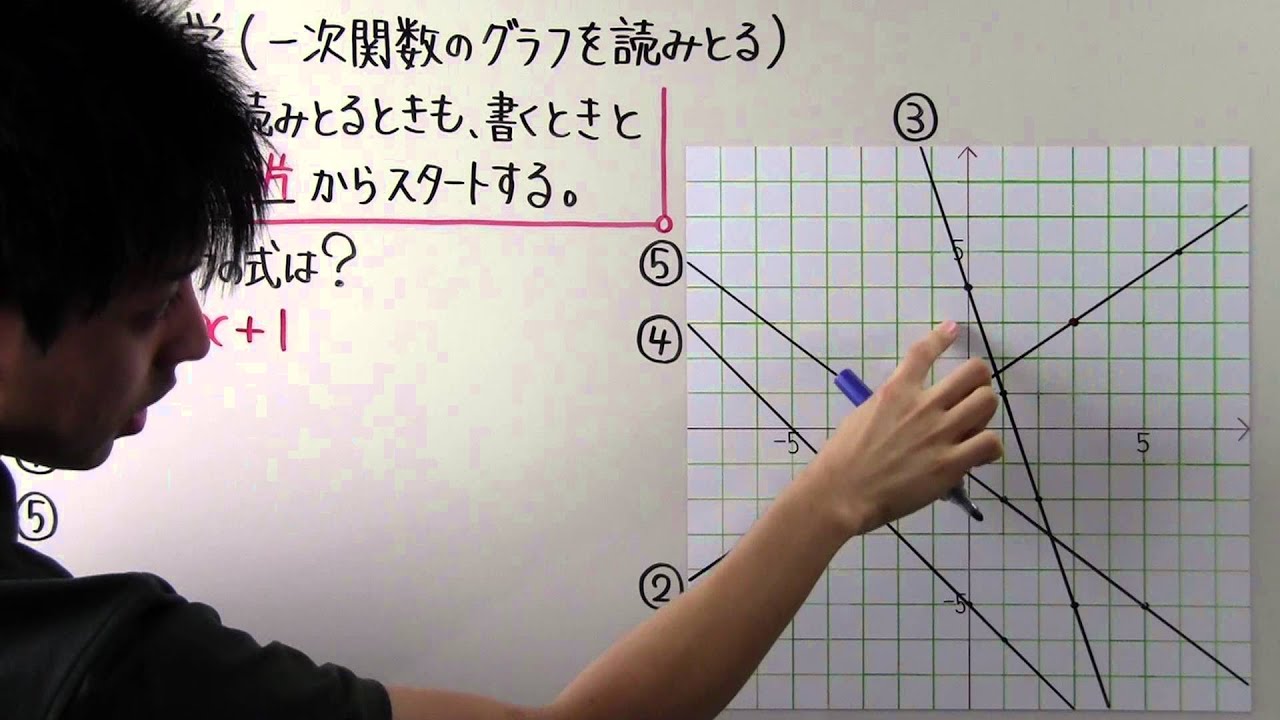 1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 | 1次関数の交点の座標とグラフから直線の方程式を求める方法 |
1次関数の交点の座標とグラフから直線の方程式を求める方法 | 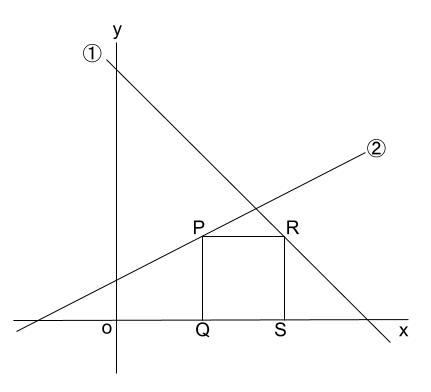 1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |
1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 | 1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 | 1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 | 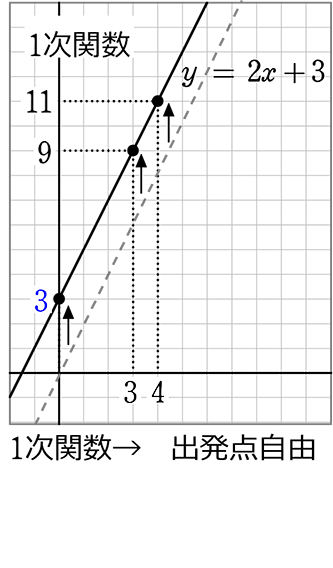 1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 | 1次関数の交点の座標とグラフから直線の方程式を求める方法 | 1次関数の交点の座標とグラフから直線の方程式を求める方法 |
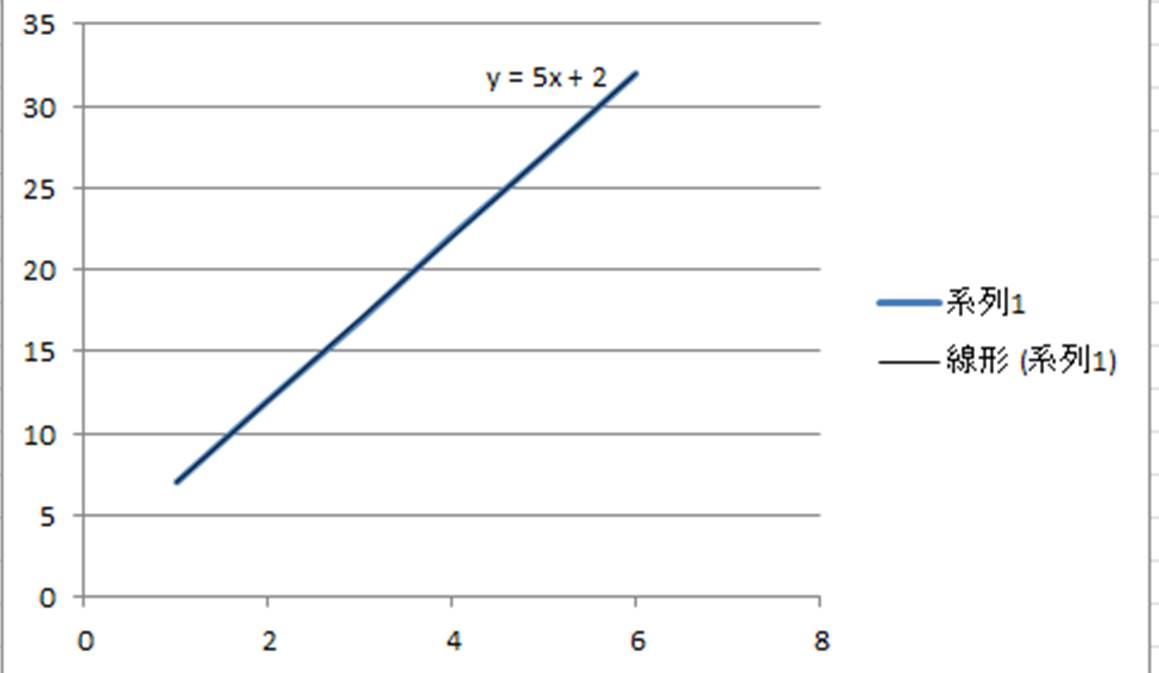 1次関数の交点の座標とグラフから直線の方程式を求める方法 | 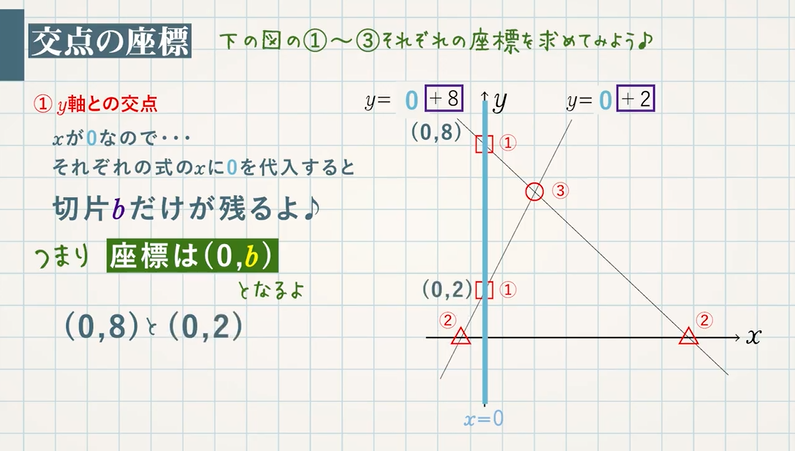 1次関数の交点の座標とグラフから直線の方程式を求める方法 | 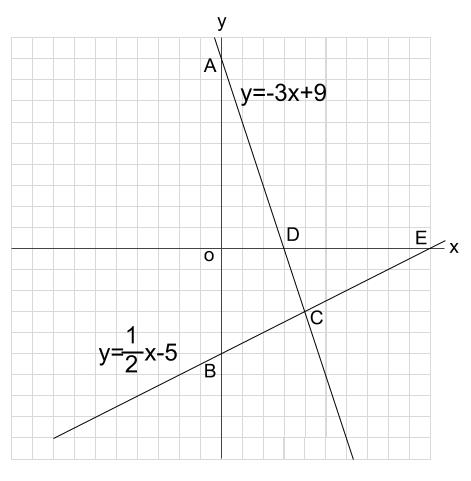 1次関数の交点の座標とグラフから直線の方程式を求める方法 |
1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 | 1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 | 1次関数の交点の座標とグラフから直線の方程式を求める方法 |
1次関数の交点の座標とグラフから直線の方程式を求める方法 | 1次関数の交点の座標とグラフから直線の方程式を求める方法 | 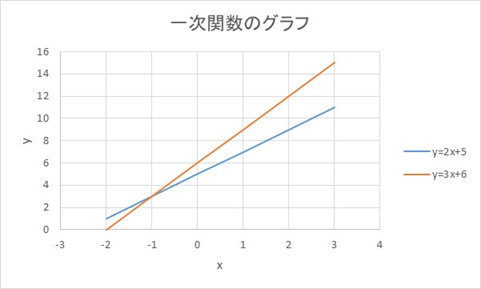 1次関数の交点の座標とグラフから直線の方程式を求める方法 |
1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 | 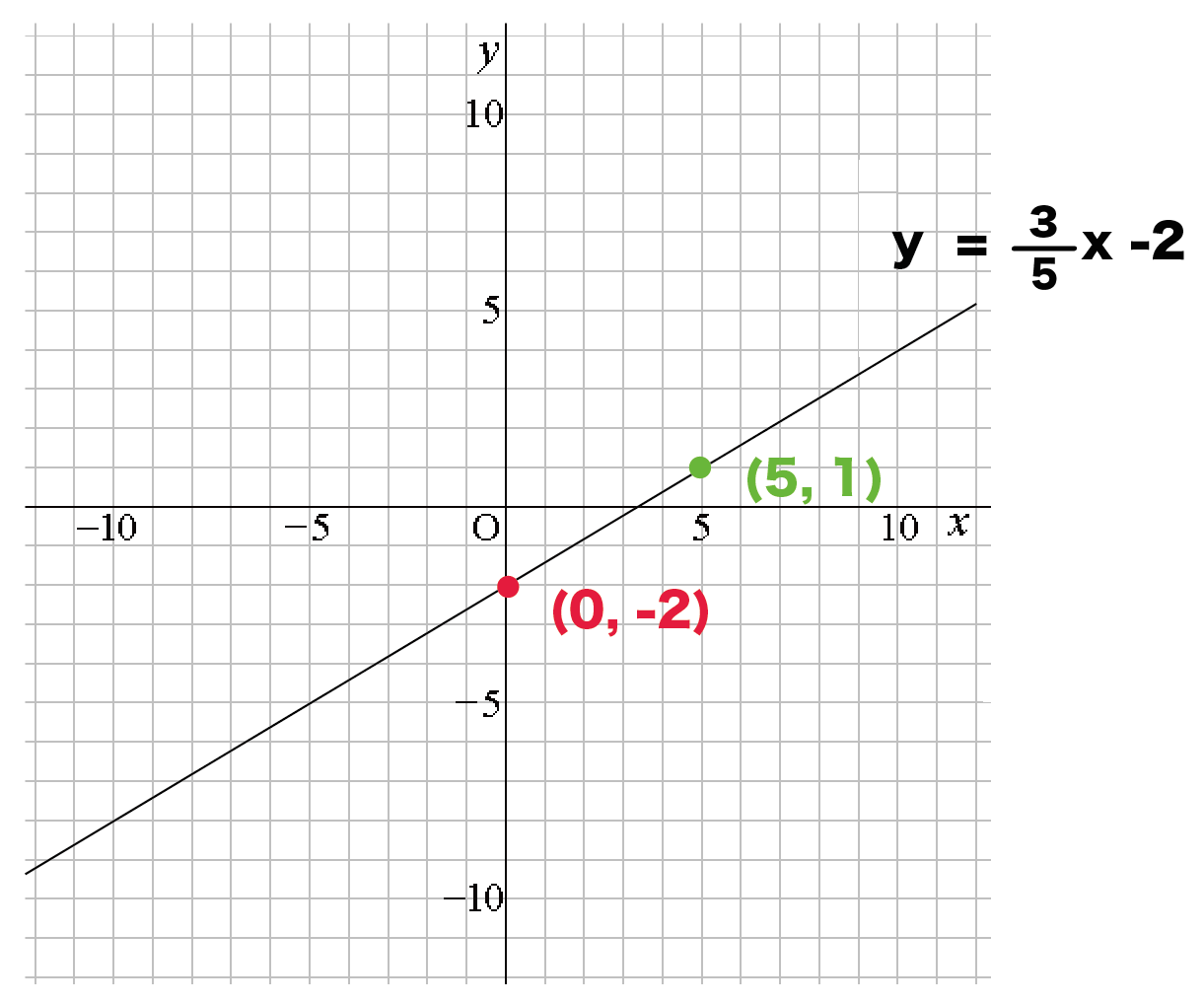 1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 |  1次関数の交点の座標とグラフから直線の方程式を求める方法 | 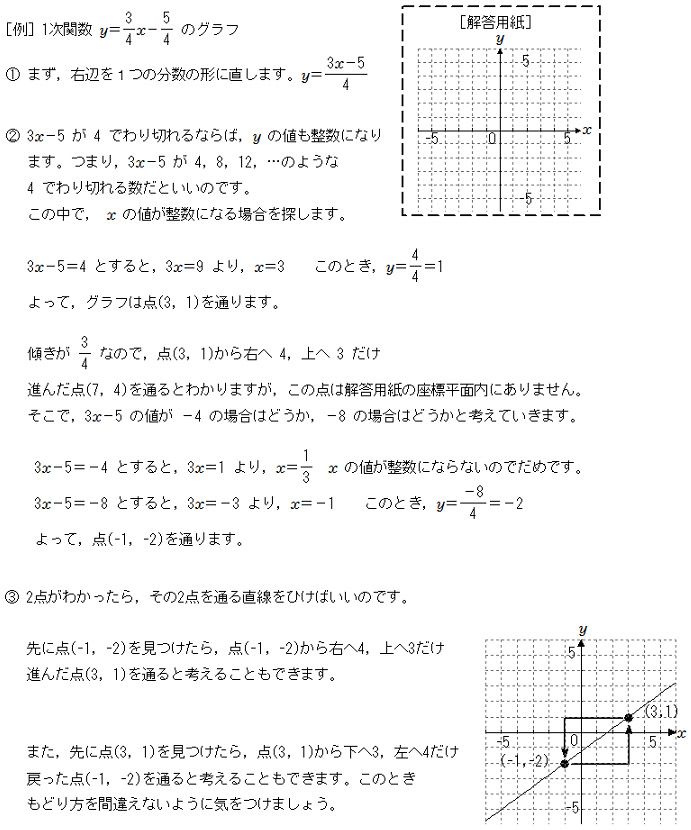 1次関数の交点の座標とグラフから直線の方程式を求める方法 |
 1次関数の交点の座標とグラフから直線の方程式を求める方法 | 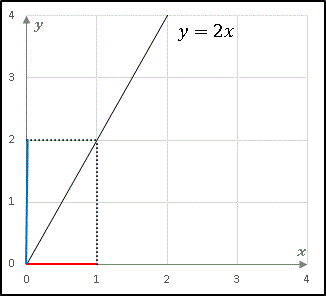 1次関数の交点の座標とグラフから直線の方程式を求める方法 |
グラフを書くために知っておくこと まずは、一次関数のグラフを書くために 知っておくべきことがあります。 x に掛けられている数を傾き 文字がついていない数だけのものを切片 (せっぺん)といいます。 傾きというのは 直線がどれくらいの増え方を1次関数のグラフの描き方は簡単です。1次関数の一般式y=axbのグラフを描きます。下記の順序に従って描きます。 ・切片の座標を点として描く(y=axbのとき切片の座標は必ず0 , bとなる)
Incoming Term: 1次関数 グラフ, 1次関数 グラフ プリント, 1次関数 グラフ エクセル, 1次関数 グラフ 文章題, 1次関数 グラフ 作成, 1次関数 グラフ 分数 解き方, 1次関数 グラフ用紙 表付き, 1次関数 グラフ 印刷, 1次関数 グラフ面白い, 1次関数 グラフ 書き方, 1次関数 グラフの書き方, 1次関数 グラフ 解き方,
コメント
コメントを投稿